Addition of Logarithms (the base a must be a positive number other than 1)
Ex.
Subtraction of Logarithms (the base a must be a positive number other than 1)
When subtracting two logarithms of equal bases, you can combine the two logs into one log with x being divided by y.
Ex.
Exponents/Coefficients of Logarithms (the base a must be a positive number other than 1)
If there is a coefficient b (which is a real number) of a log, it can be moved to be the exponent of x and vice versa.
Ex.
Change-of-Base Formula (a, b and x are positive real numbers. a and b are not 1)
If you have a log base a of x, you can change the base of the logarithm to any number that suits your needs with the log of x over the log of a. This formula is very useful for situations in which you need to calculate the numeric value of a log, but the base isn't 10 or e, which are the only two calculable on a calculator.
Ex.

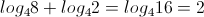






9-3-13
ReplyDelete215 Days
Love,
A106