A rational function is a function that can be written as:

where N(x) and D(x) are both polynomials, and where D(X) is not the zero multiplicity.
Ex.

When f(x)=0, the graph of a rational function is an x-intercept, this indicates that N(x)=0 and D(x) is a nonzero integer.
Ex.

; f(x)= 0 where

, such as at x=1
When D(x)=0, the graph of a rational function produces a vertical asymptote, this an undefined line which the graph will never cross.
Ex.

; When x=2, D(x)= 8-8=0, causing f(x) to be undefined and producing a vertical asymptote.
The graph below shows a rational function, the graph has a vertical asymptote on the line x=0. As you can see, the graph approaches the line x=0, but never crosses it.
Graphs of rational function can produce y-intercepts at f(0), sometimes there is a vertical asymptote at the line x=0, and therefore, the graph has no y-intercepts. This is the case in the graph above.
Ex.

; (0,-1/8) is a y-intercept of this rational function.
End Behavior
There are 3 cases for the end behavior of rational functions:
1) The degree of the leading term of N(x)>the degree of the leading term of D(x)
2) The degree of the leading term of N(x)=the degree of the leading term of D(x)
3) The degree of the leading term of N(x)<the degree of the leading term of D(x)
Each of these cases has a distinct end behavior.
1) When the degree of the numerator is larger, the end behavior of the rational function is:
Ex.

when x gets very large i.e. 1 trillion, or very small i.e. -1 trillion, no matter what the degrees of the non leading terms are, the numerator will always trump the denominator. In this case, very large negative numbers will produce positive values and approach infinity, while very large positive numbers for x will produce negative values and approach negative infinity. In this case, the limits will always be either a positive or negative infinity.
2) When the degree of the numerator is the same as the degree of the denominator, the end behavior of the rational function is a ratio of the leading coefficients of N(x) over the leading coefficients of D(x).
Ex.

no matter what the value of x is, the value can cancel, leaving only the coefficients, which simplify to a ratio of -1/3. The limit notation for this function would be:
3) When the degree of the denominator is larger than the degree of the numerator, the limit notation is always:
This is because when you plug in a very large positive or negative number into any rational function that matches this criteria, such as

, no matter what, as the magnitude of the x value increases, the value of the function will always approach zero.
***This case could also approach a different number, in rare cases, if the function had an addition or subtraction outside of the fraction which shifted the entire graph up or down.***
In cases 2 and 3, horizontals asymptotes are created, because the limits of x approach a number, such as 0, or -1/3, but never reach them. The graph above shows a horizontal asymptote at the line y=0.
A couple extra things to remember:
- The graphs of rational functions are mostly discontinuous, this means that the graph in disconnected at atleast one point. These points are usually lines, which form asymptotes. This is an important fact to remember because it may show up on a test. ;)
- If the limit of x is not positive and negative infinity, you must take this into account, often you may have indicate limit coming from the right or left side, approaching a number.
Ex.

is x approaching 3 from the right, and

is x approaching 3 from the left.
-If any x value every makes N(x)=0=D(x), there will be a hole is the graph, this value is called in-determinant and is something that must always be shown when drawing any graph of a rational function.
-C. Baller
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||///////////////////////////////////////////////////////
//////////////////////////////////////////|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

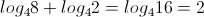







.gif)


















